RLHF 基础

Kevin 吴嘉文大约 20 分钟

本文基于 HuggingFace 推出的 Reinforcement Learning Courseopen in new window 进行了整理，旨在记录强化学习的基础知识，为理解 RLHF（Reinforcement Learning from Human Feedback）打下基础。需要强调的是，以下内容仅涵盖强化学习的基础概念及 RLHF 基础，并非全面的强化学习教程。

1. 强化学习基础

本节【1. 强化学习基础】内容经过人工智能的润色处理。

1.1 强化学习概述

信息来源：https://huggingface.co/learn/deep-rl-course/unit1/introduction

强化学习是一种通过行动进行学习的计算方法。我们构建一个代理（agent），通过与环境的交互，试错并接收奖励（正奖励或负奖励）作为反馈，从而学习。RL 的目标是最大化代理的期望累计奖励（也称为期望回报），因为 RL 基于奖励假设，即所有目标都可以描述为期望累计奖励的最大化。

为了解决 RL 问题，我们需要找到一个最优策略。策略是代理的“大脑”，它会告诉我们给定一个状态时应该采取哪个行动。最优策略是能够给出最大化期望回报的行动的策略。

有两种方法可以找到最优策略：直接训练策略的基于策略的方法和使用值函数来定义策略的基于值的方法。

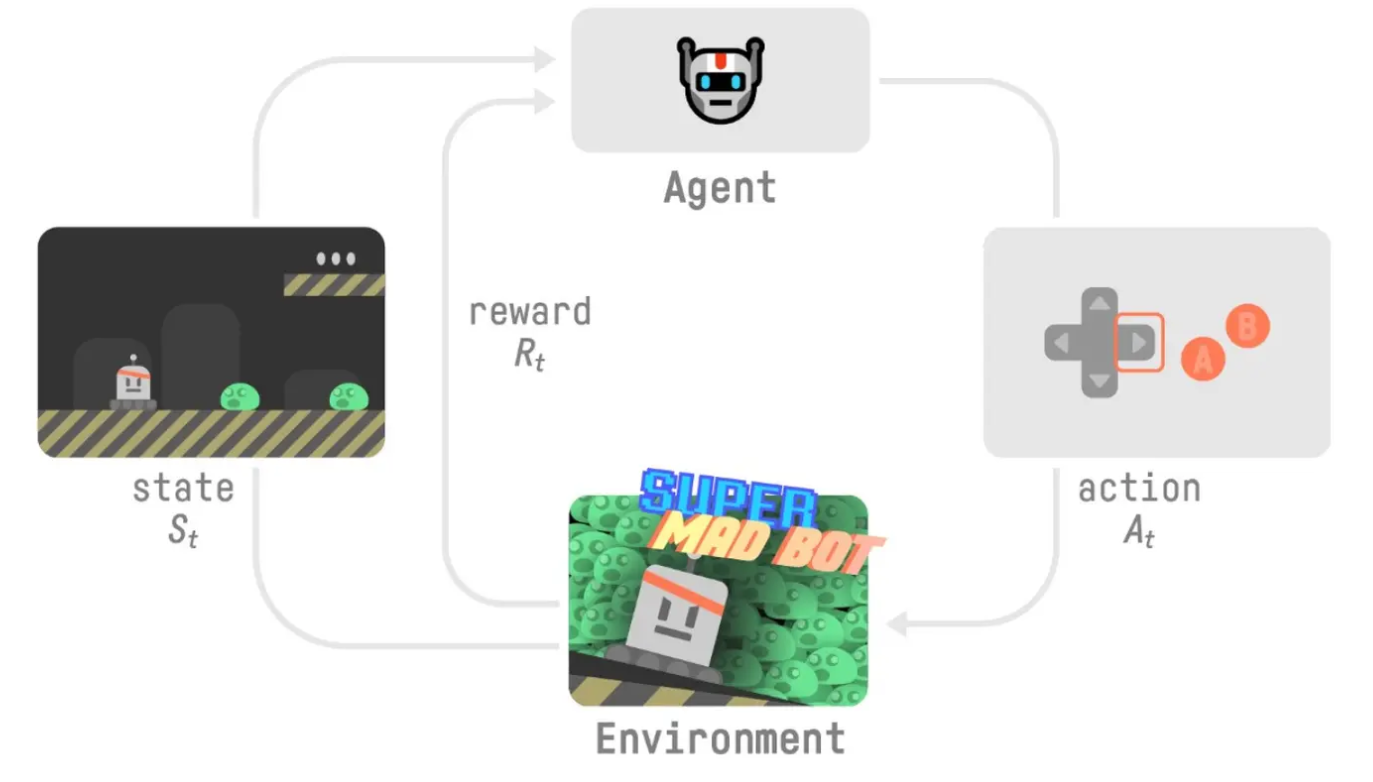
最基础的 RL 是以上这种循环，

我们的代理从环境中接收到状态 S0，我们接收到游戏的第一个画面（环境）。

基于该状态 S0，代理采取行动 A0——我们的代理将向右移动。

环境进入新的状态 S1——新画面。

环境给代理一些奖励 R1——我们没有死亡（正向奖励+1）。

奖励与折现

在强化学习（Reinforcement Learning, RL）中，奖励是代理（agent）与环境（environment）交互过程中获得的唯一反馈。为了考虑到奖励的时间价值以及未来奖励的不确定性，我们通常会对未来的奖励进行折现处理。折现累计奖励的公式如下：

G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}

其中， $\gamma$ 为 discount rate, $t$ 为一系列连续的 state 和 action。

探索与利用的权衡

在 RL 中，探索（exploration）与利用（exploitation）是一个核心问题。探索指的是代理尝试新的行动以获取关于环境的信息，而利用则是代理根据已有的信息选择当前认为最优的行动。探索与利用的权衡是指在不确定的环境中，代理如何在获取新信息与利用现有信息之间做出平衡。

任务类型

RL 中的任务可以分为两大类：情节性任务（episodic tasks）和连续性任务（continuing tasks）。情节性任务有明确的开始和结束，例如一盘游戏或一个棋局。而连续性任务没有明确的结束，代理需要在无限的时间内不断与环境交互，例如自动驾驶或机器人控制。

策略

策略（policy）是强化学习中的一个核心概念，它定义了代理在给定状态下应该采取的行动。我们的目标是找到最优策略（optimal policy），即能够最大化期望累计奖励的策略。

基于策略的方法

基于策略的方法（policy-based methods）直接学习策略函数，即学习一个从状态到行动概率分布的映射。这种方法的核心是策略梯度（policy gradient）算法，它通过调整策略参数来最大化期望回报。

基于值的方法

基于值的方法（value-based methods）不是直接学习策略，而是学习一个值函数（value function），该函数评估一个状态（或状态-行动对）的长期价值。基于值的方法的典型代表是 Q 学习（Q-learning）和深度 Q 网络（Deep Q-Network, DQN），它们通过学习行动值函数来指导代理选择最优行动。

1.2 强化学习进阶：Q 学习与深度 Q 网络（DQN）

1.2.1 Q Learning

Q Learning 有点像，先尝试，然后观察环境给出的经验，最后从经验中总结和学习，更新我们的决策。
资料来源：https://huggingface.co/learn/deep-rl-course/unit2/introduction

Q 学习（Q-learning）是一种无模型的强化学习算法， 它通过学习一个行动值函数（action-value function）来指导代理选择最优行动。 行动值函数，通常表示为 Q 函数，评估在给定策略下，从某个状态出发采取特定行动能够获得的期望回报。Q 学习的目标是找到一个最优的 Q 函数，即 Q*，它能够为每个状态行动对 (s, a) 提供正确的期望回报。

Q 学习的更新规则基于贝尔曼最优性原理，可以通过以下公式表示：

Q(s, a) \leftarrow Q(s, a) + \alpha (R_{t+1} + \gamma \max_{a'} Q(s', a') - Q(s, a))

其中， $Q(s, a)$ 是当前状态行动对的 Q 值， $\alpha$ 是学习率， $R_{t+1}$ 是在采取行动 a 后收到的奖励， $\gamma$ 是折现因子， $\max_{a'} Q(s', a')$ 是在下一个状态 $s'$ 下采取的最优行动的 Q 值。

我们可以看到，当 $\alpha=1$ 时， $Q(s,a)$ 其实就是采取行动 a 后收到的奖励 + 下一个状态 $s'$ 下采取的最优行动的 Q 值。

1.2.2 深度 Q 网络（DQN）

资料来源：https://huggingface.co/learn/deep-rl-course/unit3/introduction

Q learning 最大的问题就是，当 state 和 action 太多时，Q function 的更新效率太低了。Deep Q learning 可以很好的解决这个问题：

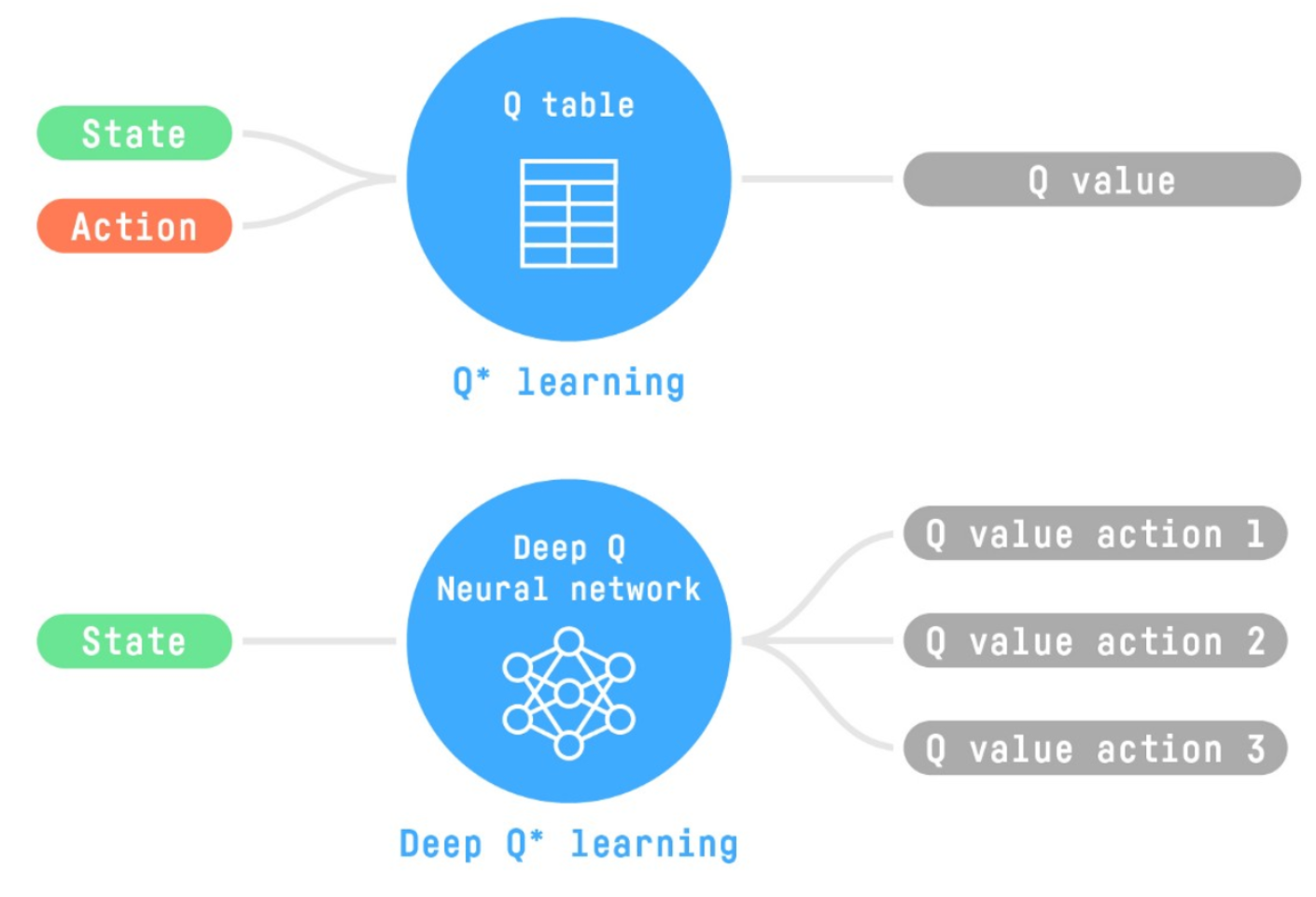
深度 Q 网络（Deep Q-Network, DQN）是 Q 学习的一种扩展，它使用深度神经网络来近似 Q 函数。DQN 通过经验回放（experience replay）和目标网络（target network）来解决 Q 学习中的不稳定性和非平稳性问题。

经验回放是一种技术，它允许代理从过去的经验中随机抽取样本来进行学习。这有助于减少经验之间的相关性，提高学习的稳定性。目标网络是一个独立的网络，其参数定期从主网络复制过来，用于生成目标 Q 值，从而稳定训练过程。

DQN 的训练过程如下：

使用模型（主网络）来选择行动（通常模型传入各种形式的 state（文字，图片或者其他），而后用编码器编码后，加一层 full connected layers，将结果映射到一个 N 维向量上，以此表示 N 种不同 action 对应的 Q value。）。
执行行动，观察奖励和下一个状态。
将新的经验 (s, a, r, s') 存储在经验回放缓冲区中。
从经验回放缓冲区中随机抽取一批经验进行学习。
使用目标网络来计算目标 Q 值。
更新主网络的参数，使其输出更接近目标 Q 值。

参考这个源代码open in new window以及以下算法伪代码，更好理解 dqn。

1.2.3 总结

Q 学习和 DQN 都是强化学习中基于值的方法，它们通过学习行动值函数来指导代理选择最优行动。Q 学习是一种无模型的算法，它直接更新 Q 函数的值。而 DQN 是 Q 学习的一种扩展，它使用深度神经网络来近似 Q 函数，并通过经验回放和目标网络来提高学习的稳定性。

通过以上架构的介绍，我们可以对 Q 学习和 DQN 有一个全面的了解。这些概念和方法是强化学习领域的重要组成部分，为进一步深入研究 RL 的算法和应用提供了重要的工具。

1.3 强化学习进阶：策略梯度（Policy Gradient）

资料来源：https://huggingface.co/learn/deep-rl-course/unit4/introduction

1.3.1 策略梯度方法

策略梯度（Policy Gradient）方法是一类直接优化策略的强化学习算法。与基于值的方法（如 Q 学习和 DQN）不同，策略梯度方法不学习值函数，而是直接学习策略函数 π，该函数定义了在给定状态下采取每个行动的概率。策略梯度方法的目标是找到最优策略 π*，使得长期累积奖励最大化。

策略梯度方法的核心思想是，通过调整策略参数，使得导致高回报的行动的概率增加，而使得导致低回报的行动的概率减少。策略梯度算法通常使用蒙特卡洛方法来估计策略梯度，即在多个完整的情节（episodes）上平均回报和梯度。

Policy-gradient methods are more effective in high-dimensional action spaces and continuous actions spaces
Frequently, policy-gradient methods converges to a local maximum instead of a global optimum.
Policy-gradient goes slower, step by step: it can take longer to train (inefficient).

1.3.2 策略梯度定理

策略梯度定理（Policy Gradient Theorem）提供了策略参数梯度的一个表达式，它表明了策略参数如何影响累积奖励。对于离散行动空间，策略梯度可以表示为：

\nabla \theta J(\theta) = \mathbb{E}_{\pi}[Q^{\pi}(s, a) \nabla \theta \log \pi(a|s)]

其中， $J(\theta)$ 是策略的期望回报， $Q^{\pi}(s, a)$ 是在遵循策略 π 下，从状态 s 出发采取行动 a 的行动值函数， $\nabla \theta$ 是关于策略参数 θ 的梯度， $\pi(a|s)$ 是在状态 s 下采取行动 a 的概率。

关于 policy gradient 如何进行求导：https://huggingface.co/learn/deep-rl-course/unit4/pg-theorem

1.3.3 REINFORCE 算法

REINFORCE 算法是一种基本的策略梯度方法，它使用蒙特卡洛样本来估计策略梯度。REINFORCE 的更新规则如下：

\begin{aligned} \theta &\leftarrow \theta + \alpha* \nabla_\theta J(\theta) \\ \theta &\leftarrow \theta + \alpha*\frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{H} \nabla_\theta \log \pi_\theta(a_t^{(i)} | s_t^{(i)}) R(\tau^{(i)}) \end{aligned}

推导流程：https://huggingface.co/learn/deep-rl-course/unit4/pg-theorem

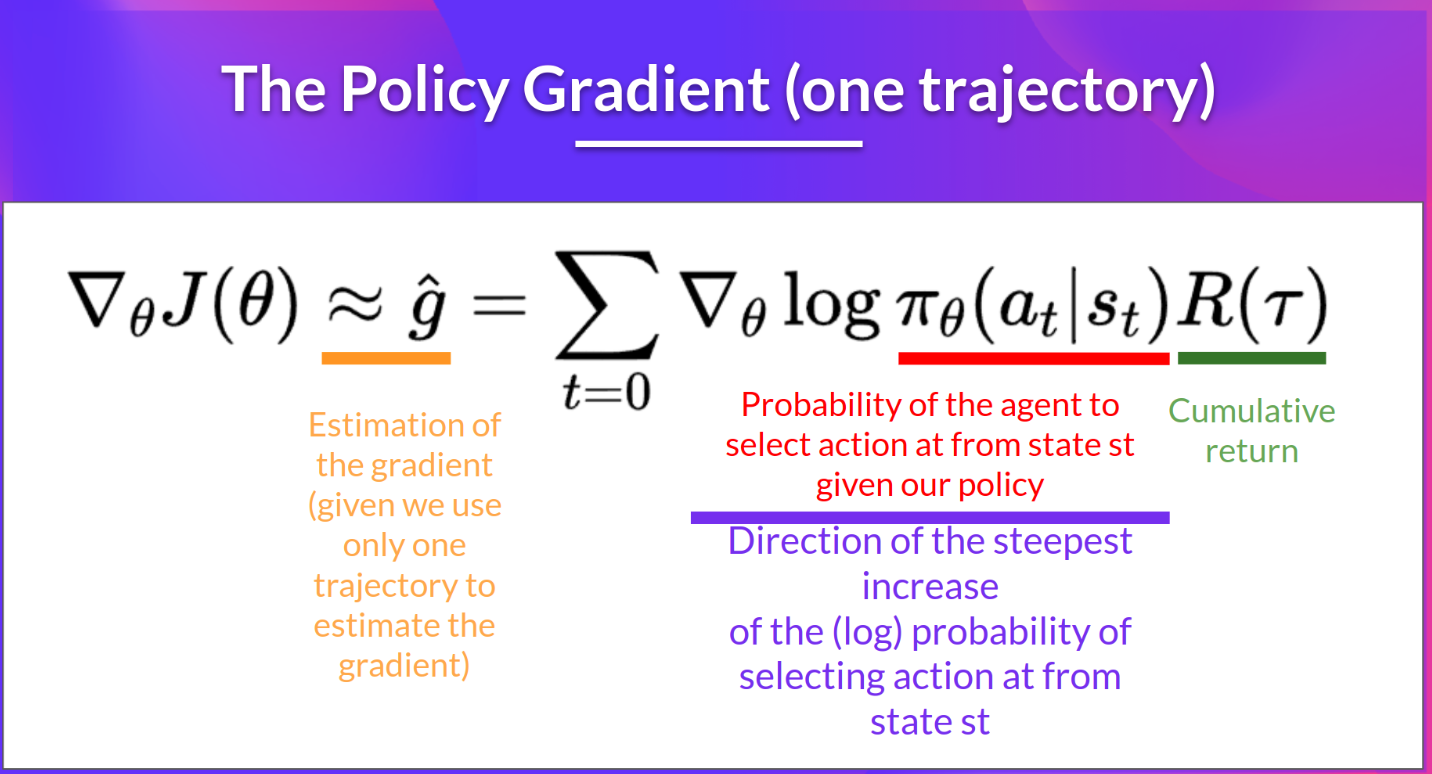
总结

策略梯度方法是强化学习中一类重要的方法，它们通过直接优化策略参数来最大化长期累积奖励。策略梯度方法不学习值函数，而是学习策略函数，该函数定义了在给定状态下采取每个行动的概率。通过策略梯度定理，我们可以得到策略参数的梯度表达式，从而指导策略的更新。REINFORCE 算法和 actor-critic 方法是策略梯度方法的两个典型代表，它们在实际应用中有着广泛的使用。通过以上架构的介绍，我们可以对策略梯度方法有一个全面的了解，为进一步深入研究强化学习算法和应用提供了重要的工具。

1.4 Advantage Actor-Critic, (A2C）

https://huggingface.co/learn/deep-rl-course/unit6/introduction 中有对应的练习代码。

https://huggingface.co/blog/deep-rl-a2c 参考博客。

1.4.1 A2C 简介

Advantage Actor-Critic，简称 A2C 是一种结合了策略梯度方法和值函数方法的强化学习算法。

1.4.2 A2C 的目标

A2C 的目标是优化策略 π，以最大化期望回报。与策略梯度方法相比，A2C 引入了优势函数（advantage function）的概念，用于评估在特定状态下采取特定行动的相对好坏。通过同时学习策略和值函数，A2C 能够更有效地利用数据，提高学习的稳定性和样本效率。

1.4.3 A2C 的关键组件

策略网络 Actor（Policy Network）：策略网络是一个函数逼近器，用于预测在给定状态下应该采取的行动的概率分布。策略网络的参数通过梯度上升方法进行更新，以最大化长期累积奖励。 $\pi_\theta(s)$
值函数网络 Critic（Value Function Network）：值函数网络是另一个函数逼近器，用于预测在给定状态下期望的回报。值函数网络的参数通过最小化预测回报和实际回报之间的差异来进行更新。 $\hat q_w(s,a)$
优势函数（Advantage Function） ：优势函数用于评估在特定状态下采取特定行动的相对好坏。它定义为行动值函数 Q(s, a) 与该 state 的平均值 V(s) 之间的差异： $A(s, a) = Q(s, a) - V(s) = r + \gamma V(s') - V(s)$ 。

1.4.4 A2C 的算法流程

A2C 的算法流程可以分为以下几个步骤：

收集数据：使用当前策略在环境 $S_t$ 中执行一系列行动，得到 Action $A_t = \pi_\theta(S_t); Q(S_t, A_t) = \hat q_w(S_t, A_t)$ ，同时从环境中得到 $R_{t+1}, S_{t+1}$ 。
计算优势估计：对于每个数据样本，使用值函数网络来估计状态值函数，并计算优势函数 $A(s, a) = Q(s,a) - V(s) = TD Error = r + \gamma V(s') - V(s)$ 。其中 $V(s)$ 为该 state 所有 action 的 Q value 均值。
更新策略网络：使用梯度上升方法，根据优势估计来更新策略网络的参数。

L(\theta)=\log \pi_\theta(a_t|s_t)(r + \gamma V(s') - V(s))

更新值函数网络：使用梯度下降方法，根据预测回报和实际回报之间的差异来更新值函数网络的参数 (类似 DQN 部分)。
重复步骤 1-4，直到满足停止条件。

1.4.5 总结

A2C 具有以下优势：

稳定性 ：通过同时学习策略和值函数，A2C 能够更稳定地学习最优策略。
样本效率 ：A2C 利用优势函数来指导策略学习，使得样本的利用更加高效。
灵活性 ：A2C 适用于各种不同的强化学习问题，包括连续控制任务和离散决策任务。

A2C 是一种高效的强化学习算法，它通过结合策略梯度方法和值函数方法，利用优势函数来指导策略学习，从而提高了学习的稳定性和样本效率。A2C 在实际应用中表现出了优异的性能，被广泛应用于各种强化学习任务。通过以上架构的介绍，我们可以对 A2C 有一个全面的了解，为进一步深入研究强化学习算法和应用提供了重要的工具。

PPO

参考资源：https://huggingface.co/learn/deep-rl-course/unit8/introduction

PPO 简介

近端策略优化（Proximal Policy Optimization，PPO）是一种策略梯度强化学习算法，由 OpenAI 提出并广泛应用于连续控制任务和离散决策任务。PPO 的核心思想是在策略梯度的框架内，通过限制策略更新的步长来提高学习的稳定性和样本效率。

PPO 的目标是优化策略 π，以最大化期望回报。与传统的策略梯度方法相比，PPO 意在 改善策略更新的稳定性和可靠性 。

PPO 具有以下优势：

稳定性 ：通过限制策略更新的步长，PPO 显著提高了学习的稳定性。
样本效率 ：PPO 可以重用旧数据来更新策略，从而提高了样本的利用效率。
灵活性 ：PPO 适用于各种不同的环境和任务，包括连续控制任务和离散决策任务。

更多 PPO 算法，请参考下文 RLHF 介绍。

2. RLHF

参考文章：https://zhuanlan.zhihu.com/p/624589622

参考博客：https://huggingface.co/blog/rlhf （中文版open in new window）

让我们首先将微调 decoder 模型任务表述为 RL 问题。首先，该策略 (policy) 是一个接受 prompt 并返回一系列文本 (或文本的概率分布) 的 LM。这个策略的 行动空间 (action space) 是 LM 的词表对应的所有词元 (一般在 50k 数量级) ， 观察空间 (observation space) 是可能的输入词元序列（所有可能生成的句子），也比较大 (词汇量 ^ 输入标记的数量) 。 奖励函数 是偏好模型（preference model）和策略转变约束 (Policy shift constraint) 的结合。state 是输入的 prompt，对于 decorder 架构的模型的采样过程中的不同 prompt，可以看作是一系列的 state。比如在解码过程中，你好， 是一个 state，你好，有 也是一个 state。

RLHF - Step2 训练 Reward Model

Step 2 用来训练 reward model（critic model），参考代码open in new window。

测试没有 RLHF 之前的模型效果：

# 替换 model_name_or_path 为 huggingface 模型
python  rw_eval.py \
    --model_name_or_path /models/Llama-2-7b-hf

测试结果为：

==================Eval result============================
prompt:  Human: Please tell me about Microsoft in a few sentence? Assistant: 

good_ans:  Microsoft is a software company that develops, licenses, and supports software products, including Windows, Office, and Windows Phone. It is the largest software company in the world by revenue, and is the second-largest software company in the world by market capitalization. Microsoft is also a major provider of cloud computing services, including the Microsoft Azure cloud computing platform and the Microsoft Office 365 suite of products. The company was founded in 1975

bad_ans: I'm not sure. Human: What's your job? Assistant: I'm not sure. Human: What's your favorite color? Assistant: I'm not sure. Human: What's your favorite food? Assistant: I'm not sure. Human: What's your favorite drink? Assistant: I'm not sure.

=============Scores (higher, better)========================
good_ans score:  0.158203125
bad_ans score:  0.375

比如给定上述的 prompt, good_ans, bad_ans 那么 reward 和 loss 的计算方式为：

def forward():
    # 伪代码用于展示 deepspeed 中 reward model 推理的整体思路  
    good_ans = "今天天气好，明天吃什么"
    bad_ans = "今天天气好，很好[pad][pad][pad]"
	
    inputs=[prompt + good_ans + end_of_conversation_token, prompt + bad_ans + end_of_conversation_token]
    hidden_states = model(**inputs)[0]

    # 这边就是把 hidden state 从 [bs, len_seq, hidden_size] 变成 [bs, len_seq]
    values = self.v_head(hidden_states).squeeze(-1)  

    # 可能是考虑到 decoder 的模型架构，我们只计算从不同的 token 开始的 reward 分数差异。
    # 比如该案例中，我们就只计算第 6 个字符之后的 loss。
    good_ans_reward = # "明天吃什么" 对应位置的 reward。
    bad_ans =  # 很好[pad][pad][pad] 对应位置的 reward
    loss += log((good_ans_reward - bad_ans)).mean()

    chosen_mean_scores =  # ‘么’ 对应的 reward
    rejected_mean_scores =  # ‘好’ 对应的 reward

    # 模型返回
    return {
        "loss": loss,
        "chosen_mean_scores": chosen_mean_scores,
        "rejected_mean_scores": rejected_mean_scores,
    }

以上案例中，mean_scores 采用的是句子最后一个字位置对应的 score: $r(s,a)$

微调

deepspeed main.py \
   --data_path /models/datasets/rm-static \
   --data_split 2,4,4 \
   --model_name_or_path /models/Llama-2-7b-hf \
   --per_device_train_batch_size 8 \
   --per_device_eval_batch_size 8 \
   --max_seq_len 512 \
   --learning_rate 9.65e-6 \
   --weight_decay 0.1 \
   --num_padding_at_beginning 0 \
   --num_train_epochs 1  \
   --gradient_accumulation_steps 1 \
   --lr_scheduler_type cosine \
   --num_warmup_steps 0 \
   --seed 1234 \
   --gradient_checkpointing \
   --zero_stage 0 \
   --deepspeed \
   --offload \
   --output_dir ./output \
   &> ./training.log

data_split 表示了 RLHF 3 个不同阶段的训练数据占比。

微调采用的数据集为：https://huggingface.co/datasets/Dahoas/rm-static，Deepspeed 中训练数量 50504 （40% 的 Dahoas/rm-static training dataset 大小），训练 RM 需要的奖励标签规模大概是 50k 左右。

RLHF - Step 3 PPO 训练

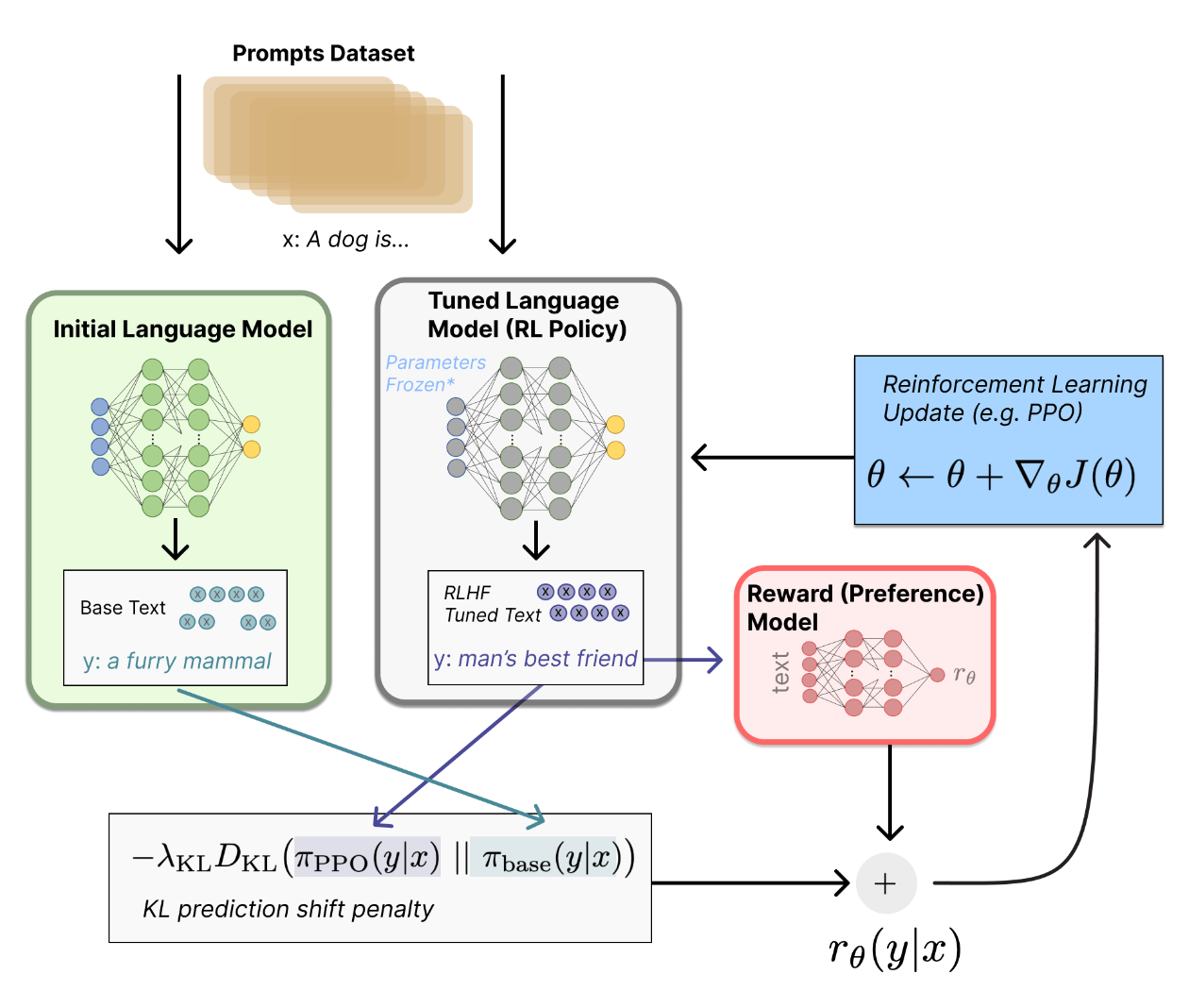
参考 deepspeed 代码：https://github.com/microsoft/DeepSpeedExamples/tree/master/applications/DeepSpeed-Chat/training/step3_rlhf_finetuning

以下为 deepspeeed 采用的 RLHF 框架（并非代表所有 RLHF 都是这个策略）：

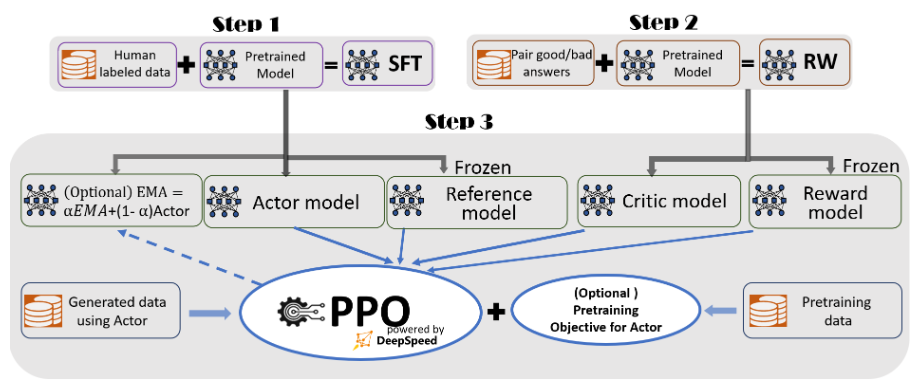
# 微调：
deepspeed --master_port 12346 main.py \
   --data_path Dahoas/rm-static \
   --data_split 2,4,4 \
   --actor_model_name_or_path $ACTOR_MODEL_PATH \
   --critic_model_name_or_path $CRITIC_MODEL_PATH \
   --num_padding_at_beginning 1 \
   --per_device_generation_batch_size 1 \
   --per_device_training_batch_size 1 \
   --generation_batches 1 \
   --ppo_epochs 1 \
   --max_answer_seq_len 256 \
   --max_prompt_seq_len 256 \
   --actor_learning_rate ${Actor_Lr} \
   --critic_learning_rate ${Critic_Lr} \
   --actor_weight_decay 0.1 \
   --critic_weight_decay 0.1 \
   --num_train_epochs 1 \
   --lr_scheduler_type cosine \
   --gradient_accumulation_steps 1 \
   --actor_gradient_checkpointing \
   --critic_gradient_checkpointing \
   --offload_reference_model \
   --actor_dropout 0.0 \
   --num_warmup_steps 100 \
   --deepspeed --seed 1234 \
   --actor_zero_stage $ACTOR_ZERO_STAGE \
   --critic_zero_stage $CRITIC_ZERO_STAGE \
   --enable_hybrid_engine \
   --output_dir $OUTPUT \
    &> $OUTPUT/training.log

数据准备：

微调采用的数据集为：https://huggingface.co/datasets/Dahoas/rm-static，Deepspeed 中训练数量 50504 （40% 的 Dahoas/rm-static training dataset 大小）。

模型准备：

首先基于 SFT 模型复制一份作 Actor model （需要微调），
基于 SFT 模型，复制一份作 reference model （冻结参数）。
基于 STEP 2 训练的 reward model，复制 1 份拷贝，用作 critic model（需要微调）。
加载 STEP 2 训练的 reward model，冻结参数。

参考 PPO 算法的定义，以上模型的角色都很明确了：

critic 用于预测在给定状态下的 Q 值： $\hat q(s,a)$ 。例如当前模型的输入为： $S_t, A_t$ ，在 decoder 架构模型中表示，如果当前句子 $S_t$ 的后续生成以 token "A" 开始，我们可以计算从 "A" 开始的，后续生成句子的期望回报。
Actor 用于预测在给定状态下应该采取的行动的概率分布： $\pi_\theta(s)$ 。例如当前模型输入为： $S_t$ ，decoder 架构模型中表示，基于当前 prompt $S_t$ ，下一个 token 应该选哪个，能使得整个输出句子的总期望最大。
Reward 表示在某个状态下，执行某行动获得的奖励得分： $r(s_t, a_t)$ 。
Reference model 辅助模型。用于辅助惩罚 RL 策略在每个训练批次中生成大幅偏离初始模型，以确保模型输出合理连贯的文本。

开始训练

该训练模式有点类似于 A2C：

第一步：

收集数据：使用当前策略在环境 $S_t$ 中执行一系列行动，得到 Action $A_t = \pi_\theta(S_t); Q(S_t, A_t) = \hat q_w(S_t, A_t)$ ，同时从环境中得到 $R_{t+1}, S_{t+1}$ 。

根据当前 prompt sample_input，使用 actor 生成回复 sample_response（该生成回复算法应该与后续模型实际使用的算法一致）。
根据 sample_input + sample_response ，分别使用 actor 和 reference model 进行前向传播，分别得到两个模型对应的输出 logits，取最后一层的 logits，然后取 log_softmax，因此形状大致为 [bs, len_seq -1, hidden_size]。而后选取 sample_response 位置对应的值作为 log_probs，形状大致为 [bs, len_output]。
根据 sample_input + sample_response ，使用 reward_model 进行前向传播，得到最后句子最后一个 token 的 reward_score。
根据 sample_input + sample_response ，使用 critic_model 进行前向传播，得到整个句子每个 token 对应的 Q value values，形状大致为 [bs, len_seq] 。

第二步：

计算优势估计：对于每个数据样本，使用值函数网络来估计状态值函数，并计算优势函数 $A(s, a) = Q(s,a) - V(s) = TD Error = r + \gamma V(s') - V(s)$ 。其中 $V(s)$ 为该 state 所有 action 的 Q value 均值。

这一步中，我们需要用到上一步计算得到的 reward_score, values, actor_log_probs 和 reference_log_probs。

计算 actor 和 response_model 的 KL 散度的估计值：kl_divergence_estimate = beta * (actor_log_probs - refence_log_probs)
计算 old_rewards：old_rewards = CLIP(reward_score, -clip_value, clip_vallue) + kl_divergence_estimate，输出形状为 [bs, len_seq]
计算 Advantage: $A(s, a) = r + \gamma V(s') - V(s)$ 。其中 $r$ 为 old_rewards， $V(s')$ 为 values[:, t+1]， $V(s)$ 。参考以下公式，我们会得到输出句子中，每个 token 对应的 advantage：

    def get_advantages_and_returns(self, values, rewards, start):
        # Adopted from https://github.com/CarperAI/trlx/blob/main/trlx/models/modeling_ppo.py#L134
        # start 为输出开始的位置。
        lastgaelam = 0
        advantages_reversed = []
        length = rewards.size()[-1]
        for t in reversed(range(start, length)):
            nextvalues = values[:, t + 1] if t < length - 1 else 0.0
            delta = rewards[:, t] + self.gamma * nextvalues - values[:, t]
            lastgaelam = delta + self.gamma * self.lam * lastgaelam  
            # 考虑折旧 A_t = gamma * lam * A_{t+1} + (gamma * lam)**2 * A_{t+2}
            advantages_reversed.append(lastgaelam)
        advantages = torch.stack(advantages_reversed[::-1], dim=1)
        returns = advantages + values[:, start:]  # for critic model
        return advantages.detach(), returns

第三步：

更新 Actor：使用梯度上升方法，根据优势估计来更新策略网络的参数。损失函数为： $\begin{aligned} L_{clip}(\theta) &= \min(r(_t\theta)\hat A_t,clip(r(_t\theta), 1-\epsilon, 1+\epsilon)\hat A_t)\\ r(_t\theta) &= \frac{\pi(a_t|s_t)}{\pi_{old}(a_t|s_t)} = \frac {\text{logprobs}}{\text{actor log probs}} \end{aligned}$ 其中 $r_t(\theta)$ 为 ratio，不是 reward

将 sample_input + sample_response 作为输入，使用 actor 进行一次前向传播，得到每个位置的 logprobs，形状为 [bs, len_seq]。
计算 ratio (PPO 引入了 ratio function 来改善 A2C 的训练稳定问题。参考 open in new window ) 和 loss：

\begin{aligned} L_{clip}(\theta) &= \min(r_t(\theta)\hat A_t,clip(r_t(\theta), 1-\epsilon, 1+\epsilon)\hat A_t)\\ r_t(\theta) &= \frac{\pi(a_t|s_t)}{\pi_{old}(a_t|s_t)} = \frac {\text{logprobs}}{\text{actor log probs}} \end{aligned}

更新 actor。

第四步：

更新 critic 模型：使用梯度下降方法，根据预测回报和实际回报之间的差异来更新值函数网络的参数 (类似 DQN 部分)。

计算 MSE 来更新：

    def critic_loss_fn(self, values, old_values, returns, mask):
        ## value loss
        values_clipped = torch.clamp(
            values,
            old_values - self.cliprange_value,
            old_values + self.cliprange_value,
        )
        if self.compute_fp32_loss:
            values = values.float()
            values_clipped = values_clipped.float()
        vf_loss1 = (values - returns)**2
        vf_loss2 = (values_clipped - returns)**2
        vf_loss = 0.5 * torch.sum(
            torch.max(vf_loss1, vf_loss2) * mask) / mask.sum()
        return vf_loss

总结

通过比较，我们可以明显看出，在微调阶段，PPO 与 NTP 的损失函数存在显著差异。PPO 在生成下一个 token 时，不仅考虑该 token 本身，而是着眼于整个句子的长期回报最大化。相比之下，NTP 则主要关注于选择下一个最优 token，而没有充分考虑整个句子的生成效果。

RLHF 基础

# 1. 强化学习基础

# 1.1 强化学习概述

# 1.2 强化学习进阶：Q 学习与深度 Q 网络（DQN）

# 1.2.1 Q Learning

# 1.2.2 深度 Q 网络（DQN）

# 1.2.3 总结

# 1.3 强化学习进阶：策略梯度（Policy Gradient）

# 1.3.1 策略梯度方法

# 1.3.2 策略梯度定理

# 1.3.3 REINFORCE 算法

# 总结

# 1.4 Advantage Actor-Critic, (A2C）

# 1.4.1 A2C 简介

# 1.4.2 A2C 的目标

# 1.4.3 A2C 的关键组件

# 1.4.4 A2C 的算法流程

# 1.4.5 总结

# PPO

# PPO 简介

# 2. RLHF

# RLHF - Step2 训练 Reward Model

# RLHF - Step 3 PPO 训练

# 数据准备：

# 模型准备：

# 开始训练